12.1 The ellipse (Page 3/16)

<< Chapter < Page

Algebra and trigonometry

Page 3 / 16

Chapter >> Page >

A General Note

Standard forms of the equation of an ellipse with center (0,0)

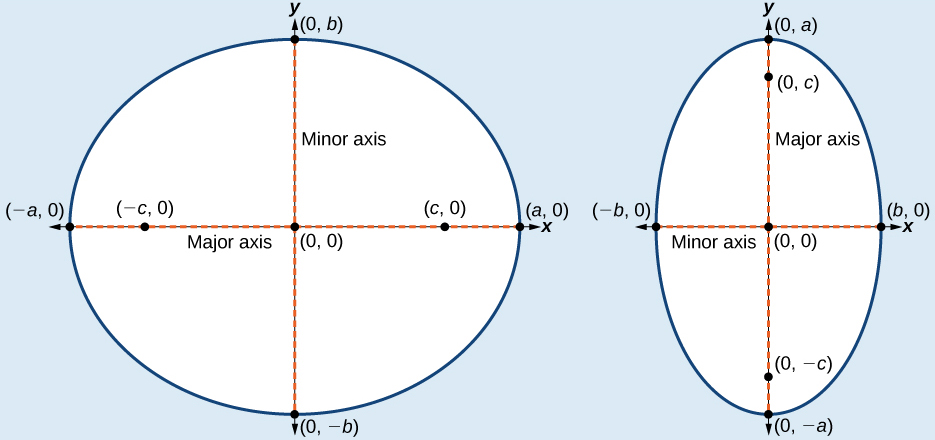
The standard form of the equation of an ellipse with center $(0, 0)$ and major axis on the x-axis is

$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

where

$a > b$
the length of the major axis is $2 a$
the coordinates of the vertices are $(\pm a, 0)$
the length of the minor axis is $2 b$
the coordinates of the co-vertices are $(0, \pm b)$
the coordinates of the foci are $(\pm c, 0)$ , where $c^{2} = a^{2} - b^{2} .$ See [link] a

The standard form of the equation of an ellipse with center $(0, 0)$ and major axis on the y-axis is

$\frac{x^{2}}{b^{2}} + \frac{y^{2}}{a^{2}} = 1$

where

$a > b$
the length of the major axis is $2 a$
the coordinates of the vertices are $(0, \pm a)$
the length of the minor axis is $2 b$
the coordinates of the co-vertices are $(\pm b, 0)$
the coordinates of the foci are $(0, \pm c)$ , where $c^{2} = a^{2} - b^{2} .$ See [link] b

Note that the vertices, co-vertices, and foci are related by the equation $c^{2} = a^{2} - b^{2} .$ When we are given the coordinates of the foci and vertices of an ellipse, we can use this relationship to find the equation of the ellipse in standard form.

(a) Horizontal ellipse with center $(0, 0)$ (b) Vertical ellipse with center $(0, 0)$

How To

Given the vertices and foci of an ellipse centered at the origin, write its equation in standard form.

Determine whether the major axis lies on the x - or y -axis.
1. If the given coordinates of the vertices and foci have the form $(\pm a, 0)$ and $(\pm c, 0)$ respectively, then the major axis is the x -axis. Use the standard form $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1.$
2. If the given coordinates of the vertices and foci have the form $(0, \pm a)$ and $(\pm c, 0),$ respectively, then the major axis is the y -axis. Use the standard form $\frac{x^{2}}{b^{2}} + \frac{y^{2}}{a^{2}} = 1.$
Use the equation $c^{2} = a^{2} - b^{2},$ along with the given coordinates of the vertices and foci, to solve for $b^{2} .$
Substitute the values for $a^{2}$ and $b^{2}$ into the standard form of the equation determined in Step 1.

Writing the equation of an ellipse centered at the origin in standard form

What is the standard form equation of the ellipse that has vertices $(\pm 8, 0)$ and foci $(\pm 5, 0) ?$

The foci are on the x -axis, so the major axis is the x -axis. Thus, the equation will have the form

$\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$

The vertices are $(\pm 8, 0),$ so $a = 8$ and $a^{2} = 64.$

The foci are $(\pm 5, 0),$ so $c = 5$ and $c^{2} = 25.$

We know that the vertices and foci are related by the equation $c^{2} = a^{2} - b^{2} .$ Solving for $b^{2},$ we have:

$\begin{array}{l} c^{2} = a^{2} - b^{2} \\ 25 = 64 - b^{2} \begin{matrix} \end{matrix} & Substitute for c^{2} and a^{2} . \\ b^{2} = 39 & Solve for b^{2} . \end{array}$

Now we need only substitute $a^{2} = 64$ and $b^{2} = 39$ into the standard form of the equation. The equation of the ellipse is $\frac{x^{2}}{64} + \frac{y^{2}}{39} = 1.$

Got questions? Get instant answers now!

Try It

What is the standard form equation of the ellipse that has vertices $(0, \pm 4)$ and foci $(0, \pm \sqrt{15}) ?$

$x^{2} + \frac{y^{2}}{16} = 1$

Got questions? Get instant answers now!

Q&A

Can we write the equation of an ellipse centered at the origin given coordinates of just one focus and vertex?

Yes. Ellipses are symmetrical, so the coordinates of the vertices of an ellipse centered around the origin will always have the form $(\pm a, 0)$ or $(0, \pm a) .$ Similarly, the coordinates of the foci will always have the form $(\pm c, 0)$ or $(0, \pm c) .$ Knowing this, we can use $a$ and $c$ from the given points, along with the equation $c^{2} = a^{2} - b^{2},$ to find $b^{2} .$

Writing equations of ellipses not centered at the origin

Like the graphs of other equations, the graph of an ellipse can be translated. If an ellipse is translated $h$ units horizontally and $k$ units vertically, the center of the ellipse will be $(h, k) .$ This translation results in the standard form of the equation we saw previously, with $x$ replaced by $(x - h)$ and y replaced by $(y - k) .$

<< Chapter < Page Page > Chapter >>

Practice Key Terms 7

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Algebra and trigonometry. OpenStax CNX. Nov 14, 2016 Download for free at https://legacy.cnx.org/content/col11758/1.6

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?

Ask

	5 Graphing ellipses centered at the origin By OpenStax Read Online Course
	3 Writing equations of ellipses centered at the origin in standard By OpenStax Read Online Course
	Thermal-Fluid Systems MCQ By Steve Gibbs Start Quiz
©flickr: Clive	Sports Psych. Research Methods By Dakota Bocan Start Flashcards
	Are you a 5sos fan? By Rylee Minllic Start Quiz
	Negotiations Conflict Management BUS403 By Charles Jumper Start Quiz
	Fluid Mechanics MCQ By Stephanie Redfern Start Quiz
	9 AP 09 Joints MCQ Quiz By OpenStax Start Quiz
	35 Biology 35 The Nervous System MCQ By OpenStax Start Quiz
	5 AP Key Terms 05 The Integumentary System By OpenStax Start Key Terms
	32 Biology 32 Plant Reproduction MCQ By OpenStax Start Quiz
	45 Biology 45 Population and Community Ecology MCQ By OpenStax Start Quiz