| << Chapter < Page | Chapter >> Page > |
For the following exercises, use function composition to verify that f(x) and g(x) are inverse functions.
f(x)=−3x+5 and g(x)=x−5−3
For the following exercises, use a graphing utility to determine whether each function is one-to-one.
f(x)=3√3x+1
f(x)=x3−27
For the following exercises, determine whether the graph represents a one-to-one function.
For the following exercises, use the graph of f shown in [link] .
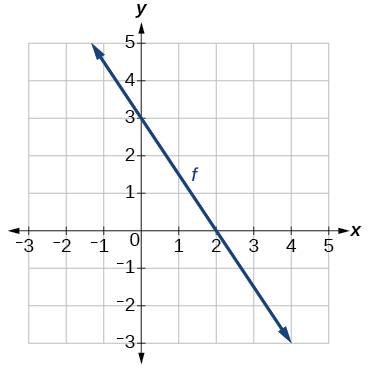
Solve f(x)=0.
Solve f−1(x)=0.
For the following exercises, use the graph of the one-to-one function shown in [link] .
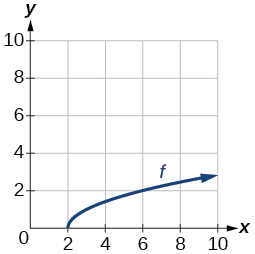
Find f(6) and f−1(2).
If the complete graph of f is shown, find the domain of f.
[2,10]
If the complete graph of f is shown, find the range of f.
For the following exercises, evaluate or solve, assuming that the function f is one-to-one.
If f(3)=2, find f−1(2).
If f−1(−2)=−1, find f(−1).
For the following exercises, use the values listed in [link] to evaluate or solve.
| x | f(x) |
|---|---|
| 0 | 8 |
| 1 | 0 |
| 2 | 7 |
| 3 | 4 |
| 4 | 2 |
| 5 | 6 |
| 6 | 5 |
| 7 | 3 |
| 8 | 9 |
| 9 | 1 |
Solve f(x)=3.
Solve f−1(x)=7.
Use the tabular representation of f in [link] to create a table for f−1(x).
| x | 3 | 6 | 9 | 13 | 14 |
| f(x) | 1 | 4 | 7 | 12 | 16 |
| x | 1 | 4 | 7 | 12 | 16 |
| f−1(x) | 3 | 6 | 9 | 13 | 14 |
For the following exercises, find the inverse function. Then, graph the function and its inverse.
f(x)=3x−2
Find the inverse function of f(x)=1x−1. Use a graphing utility to find its domain and range. Write the domain and range in interval notation.
To convert from x degrees Celsius to y degrees Fahrenheit, we use the formula f(x)=95x+32. Find the inverse function, if it exists, and explain its meaning.
f−1(x)=59(x−32). Given the Fahrenheit temperature, x, this formula allows you to calculate the Celsius temperature.
The circumference C of a circle is a function of its radius given by C(r)=2πr. Express the radius of a circle as a function of its circumference. Call this function r(C). Find r(36π) and interpret its meaning.
A car travels at a constant speed of 50 miles per hour. The distance the car travels in miles is a function of time, t, in hours given by d(t)=50t. Find the inverse function by expressing the time of travel in terms of the distance traveled. Call this function t(d). Find t(180) and interpret its meaning.
t(d)=d50, t(180)=18050. The time for the car to travel 180 miles is 3.6 hours.
For the following exercises, determine whether the relation is a function.
{(5,2),(6,1),(6,2),(4,8)}
y2+4=x, for x the independent variable and y the dependent variable
not a function
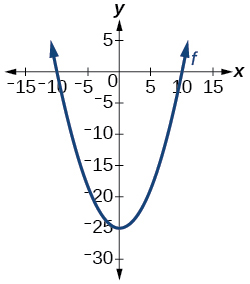
Is the graph in [link] a function?
For the following exercises, evaluate the function at the indicated values: f(−3); f(2); f(−a); −f(a); f(a+h).
f(x)=−2x2+3x
f(−3)=−27;
f(2)=−2;
f(−a)=−2a2−3a;
−f(a)=2a2−3a;
f(a+h)=−2a2+3a−4ah+3h−2h2
f(x)=2|3x−1|
For the following exercises, determine whether the functions are one-to-one.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?