10.7 Parametric equations: graphs

Algebra and trigonometry Page 1 / 4

In this section you will:

Graph plane curves described by parametric equations by plotting points.
Graph parametric equations.

It is the bottom of the ninth inning, with two outs and two men on base. The home team is losing by two runs. The batter swings and hits the baseball at 140 feet per second and at an angle of approximately $45°$ to the horizontal. How far will the ball travel? Will it clear the fence for a game-winning home run? The outcome may depend partly on other factors (for example, the wind), but mathematicians can model the path of a projectile and predict approximately how far it will travel using parametric equations . In this section, we’ll discuss parametric equations and some common applications, such as projectile motion problems.

Photo of a baseball batter swinging. — Parametric equations can model the path of a projectile. (credit: Paul Kreher, Flickr)

Graphing parametric equations by plotting points

In lieu of a graphing calculator or a computer graphing program, plotting points to represent the graph of an equation is the standard method. As long as we are careful in calculating the values, point-plotting is highly dependable.

How To

Given a pair of parametric equations, sketch a graph by plotting points.

Construct a table with three columns: $t, x (t), and y (t) .$
Evaluate $x$ and $y$ for values of $t$ over the interval for which the functions are defined.
Plot the resulting pairs $(x, y) .$

Sketching the graph of a pair of parametric equations by plotting points

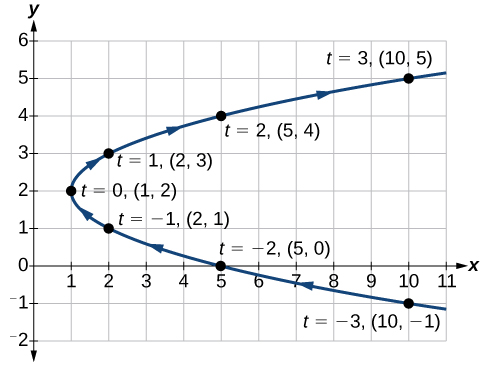
Sketch the graph of the parametric equations $x (t) = t^{2} + 1, y (t) = 2 + t .$

Construct a table of values for $t, x (t),$ and $y (t),$ as in [link] , and plot the points in a plane.

$t$	$x (t) = t^{2} + 1$	$y (t) = 2 + t$
$- 5$	$26$	$- 3$
$- 4$	$17$	$- 2$
$- 3$	$10$	$- 1$
$- 2$	$5$	$0$
$- 1$	$2$	$1$
$0$	$1$	$2$
$1$	$2$	$3$
$2$	$5$	$4$
$3$	$10$	$5$
$4$	$17$	$6$
$5$	$26$	$7$

The graph is a parabola with vertex at the point $(1, 2),$ opening to the right. See [link] .

Graph of the given parabola opening to the right.

Got questions? Get instant answers now!

Try It

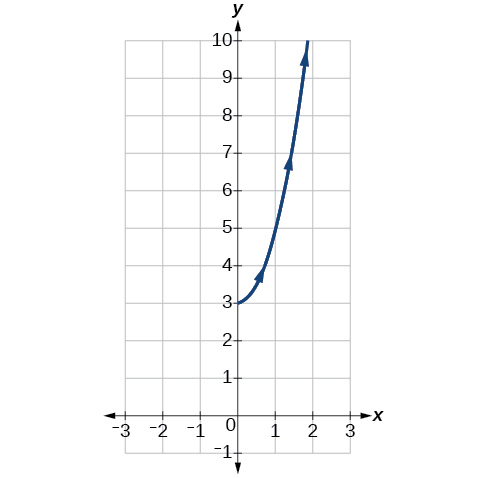
Sketch the graph of the parametric equations $x = \sqrt{t}, y = 2 t + 3, 0 \leq t \leq 3.$

Graph of the given parametric equations with the restricted domain - it looks like the right half of an upward opening parabola.

Got questions? Get instant answers now!

Sketching the graph of trigonometric parametric equations

Construct a table of values for the given parametric equations and sketch the graph:

$\begin{array}{l} \begin{array}{l} x = 2 \cos t \\ y = 4 \sin t \end{array} \end{array}$

Construct a table like that in [link] using angle measure in radians as inputs for $t,$ and evaluating $x$ and $y .$ Using angles with known sine and cosine values for $t$ makes calculations easier.

$t$	$x = 2 \cos t$	$y = 4 \sin t$
0	$x = 2 \cos (0) = 2$	$y = 4 \sin (0) = 0$
$\frac{π}{6}$	$x = 2 \cos (\frac{π}{6}) = \sqrt{3}$	$y = 4 \sin (\frac{π}{6}) = 2$
$\frac{π}{3}$	$x = 2 \cos (\frac{π}{3}) = 1$	$y = 4 \sin (\frac{π}{3}) = 2 \sqrt{3}$
$\frac{π}{2}$	$x = 2 \cos (\frac{π}{2}) = 0$	$y = 4 \sin (\frac{π}{2}) = 4$
$\frac{2 π}{3}$	$x = 2 \cos (\frac{2 π}{3}) = - 1$	$y = 4 \sin (\frac{2 π}{3}) = 2 \sqrt{3}$
$\frac{5 π}{6}$	$x = 2 \cos (\frac{5 π}{6}) = - \sqrt{3}$	$y = 4 \sin (\frac{5 π}{6}) = 2$
$π$	$x = 2 \cos (π) = - 2$	$y = 4 \sin (π) = 0$
$\frac{7 π}{6}$	$x = 2 \cos (\frac{7 π}{6}) = - \sqrt{3}$	$y = 4 \sin (\frac{7 π}{6}) = - 2$
$\frac{4 π}{3}$	$x = 2 \cos (\frac{4 π}{3}) = - 1$	$y = 4 \sin (\frac{4 π}{3}) = - 2 \sqrt{3}$
$\frac{3 π}{2}$	$x = 2 \cos (\frac{3 π}{2}) = 0$	$y = 4 \sin (\frac{3 π}{2}) = - 4$
$\frac{5 π}{3}$	$x = 2 \cos (\frac{5 π}{3}) = 1$	$y = 4 \sin (\frac{5 π}{3}) = - 2 \sqrt{3}$
$\frac{11 π}{6}$	$x = 2 \cos (\frac{11 π}{6}) = \sqrt{3}$	$y = 4 \sin (\frac{11 π}{6}) = - 2$
$2 π$	$x = 2 \cos (2 π) = 2$	$y = 4 \sin (2 π) = 0$

[link] shows the graph.

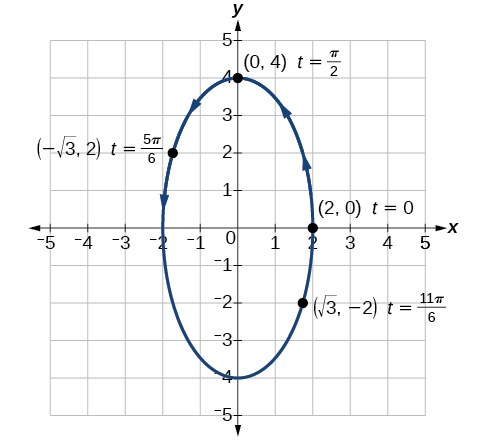
Graph of the given equations - a vertical ellipse.

By the symmetry shown in the values of $x$ and $y,$ we see that the parametric equations represent an ellipse . The ellipse is mapped in a counterclockwise direction as shown by the arrows indicating increasing $t$ values.

Got questions? Get instant answers now!

Try It

Graph the parametric equations: $x = 5 \cos t, y = 3 \sin t .$

Graph of the given equations - a horizontal ellipse.

Got questions? Get instant answers now!

Graphing parametric equations and rectangular form together

Graph the parametric equations $x = 5 \cos t$ and $y = 2 \sin t .$ First, construct the graph using data points generated from the parametric form . Then graph the rectangular form of the equation. Compare the two graphs.

Construct a table of values like that in [link] .

$t$	$x = 5 \cos t$	$y = 2 \sin t$
$0$	$x = 5 \cos (0) = 5$	$y = 2 \sin (0) = 0$
$1$	$x = 5 \cos (1) \approx 2.7$	$y = 2 \sin (1) \approx 1.7$
$2$	$x = 5 \cos (2) \approx −2.1$	$y = 2 \sin (2) \approx 1.8$
$3$	$x = 5 \cos (3) \approx −4.95$	$y = 2 \sin (3) \approx 0.28$
$4$	$x = 5 \cos (4) \approx −3.3$	$y = 2 \sin (4) \approx −1.5$
$5$	$x = 5 \cos (5) \approx 1.4$	$y = 2 \sin (5) \approx −1.9$
$−1$	$x = 5 \cos (−1) \approx 2.7$	$y = 2 \sin (−1) \approx −1.7$
$−2$	$x = 5 \cos (−2) \approx −2.1$	$y = 2 \sin (−2) \approx −1.8$
$−3$	$x = 5 \cos (−3) \approx −4.95$	$y = 2 \sin (−3) \approx −0.28$
$−4$	$x = 5 \cos (−4) \approx −3.3$	$y = 2 \sin (−4) \approx 1.5$
$−5$	$x = 5 \cos (−5) \approx 1.4$	$y = 2 \sin (−5) \approx 1.9$

Plot the $(x, y)$ values from the table. See [link] .

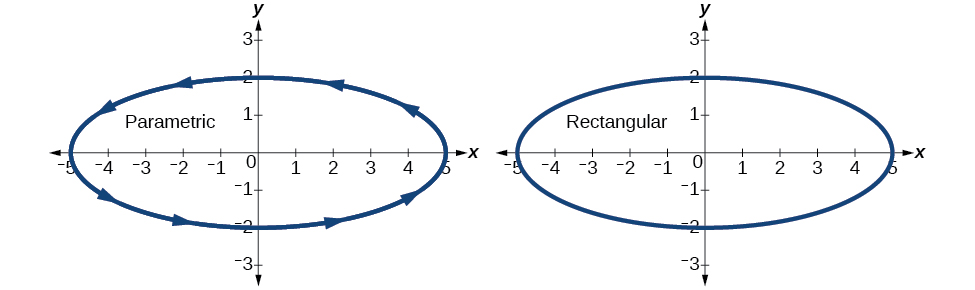
Graph of the given ellipse in parametric and rectangular coordinates - it is the same thing in both images.

Next, translate the parametric equations to rectangular form. To do this, we solve for $t$ in either $x (t)$ or $y (t),$ and then substitute the expression for $t$ in the other equation. The result will be a function $y (x)$ if solving for $t$ as a function of $x,$ or $x (y)$ if solving for $t$ as a function of $y .$

$\begin{array}{l} x = 5 \cos t \\ \frac{x}{5} = \cos t & Solve for \cos t . \\ y = 2 \sin t \begin{matrix} \end{matrix} & Solve for \sin t . \\ \frac{y}{2} = \sin t \end{array}$

Then, use the Pythagorean Theorem .

$\begin{array}{r} \cos^{2} t + \sin^{2} t = 1 \\ {(\frac{x}{5})}^{2} + {(\frac{y}{2})}^{2} = 1 \\ \frac{x^{2}}{25} + \frac{y^{2}}{4} = 1 \end{array}$

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Algebra and trigonometry. OpenStax CNX. Nov 14, 2016 Download for free at https://legacy.cnx.org/content/col11758/1.6

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?

Ask

	2 Parametric equations: graphs By OpenStax Read Online Course
	4 Microbiology Final 4 By Madison Christian Start Quiz
	3 CDL Quiz - General Knowledge Part 1 By Jazzycazz Jackson Start Quiz
	1 SCJP/OCJP Java Certification By JavaChamp Team Start Exam
	Principles of Marketing By Dionne Mahaffey Start Quiz
	2 Human A&P 2- Test 2 By Madison Christian Start Flashcards
	4 Neuroanatomy 04 Spinal Cord Brain Stem By Stephen Voron Start Quiz
	16 AP 16 Neurological Essay Exam By OpenStax Start Flashcards
	16 Biology 16 Gene Expression MCQ By OpenStax Start Quiz
	Principles of economics By OpenStax Read Online Course
	Business fundamentals By OpenStax Read Online Course