| << Chapter < Page | Chapter >> Page > |
Many applications of the derivative involve determining the rate of change at a given instant of a function with the independent variable time—which is why the term instantaneous is used. Consider the height of a ball tossed upward with an initial velocity of 64 feet per second, given by s(t)=−16t2+64t+6, where t is measured in seconds and s(t) is measured in feet. We know the path is that of a parabola. The derivative will tell us how the height is changing at any given point in time. The height of the ball is shown in [link] as a function of time. In physics, we call this the “ s - t graph.”
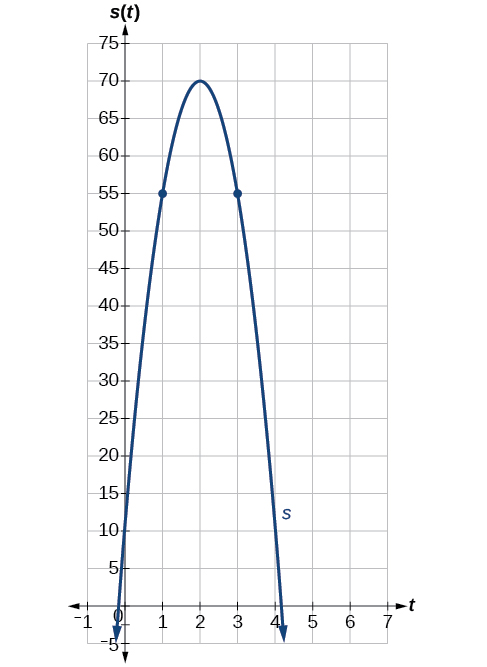
Using the function above, s(t)=−16t2+64t+6, what is the instantaneous velocity of the ball at 1 second and 3 seconds into its flight?
The velocity at t=1 and t=3 is the instantaneous rate of change of distance per time, or velocity. Notice that the initial height is 6 feet. To find the instantaneous velocity, we find the derivative and evaluate it at t=1 and t=3:
f′(a)=limh → 0 f(a+h)−f(a)h =limh → 0 −16(t+h)2+64(t+h)+6−(−16t2+64t+6)hSubstitute s(t+h) and s(t). =lim h → 0−16t2−32ht−h2+64t+64h+6+16t2−64t−6hDistribute. =limh → 0 −32ht−h2+64hhSimplify. =limh → 0 h(−32t−h+64)hFactor the numerator. =limh → 0−32t−h+64Cancel out the common factor h. s′(t)=−32t+64Evaluate the limit by letting h=0.
For any value of t , s′(t) tells us the velocity at that value of t.
Evaluate t=1 and t=3.
The velocity of the ball after 1 second is 32 feet per second, as it is on the way up.
The velocity of the ball after 3 seconds is −32 feet per second, as it is on the way down.
The position of the ball is given by s(t)=−16t2+64t+6. What is its velocity 2 seconds into flight?
0
We can estimate an instantaneous rate of change at x=a by observing the slope of the curve of the function f(x) at x=a. We do this by drawing a line tangent to the function at x=a and finding its slope.
Given a graph of a function f(x), find the instantaneous rate of change of the function at x=a.
From the graph of the function y=f(x) presented in [link] , estimate each of the following:
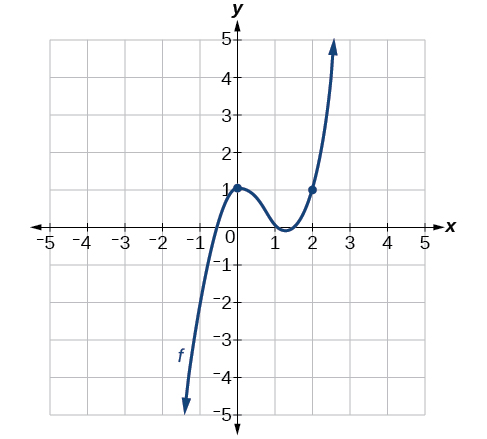
To find the functional value, f(a), find the y -coordinate at x=a.
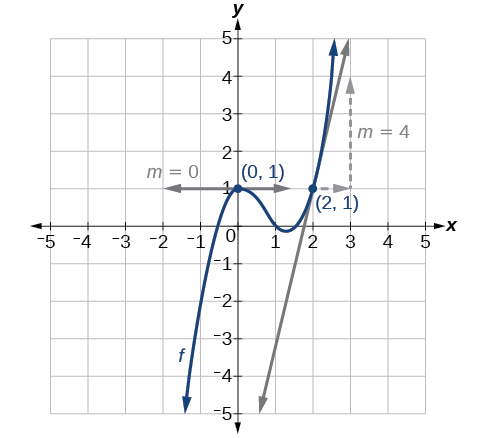
To find the derivative at x=a, f′(a), draw a tangent line at x=a, and estimate the slope of that tangent line. See [link] .

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?