| << Chapter < Page | Chapter >> Page > |
On these restricted domains, we can define the inverse trigonometric functions .
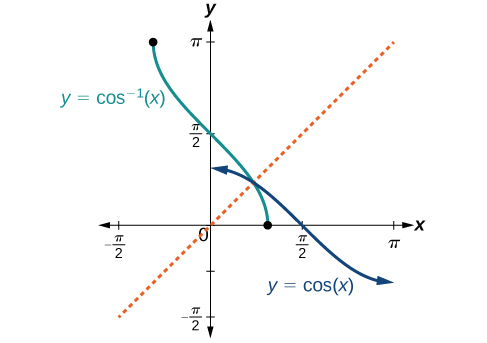
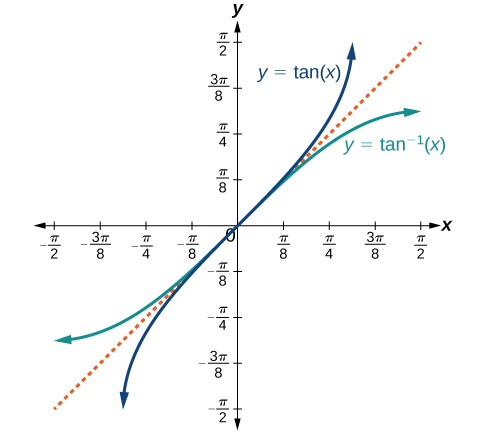
The graphs of the inverse functions are shown in [link] , [link] , and [link] . Notice that the output of each of these inverse functions is a number, an angle in radian measure. We see that sin−1x has domain [−1,1] and range [−π2,π2], cos−1x has domain [−1,1] and range [0,π], and tan−1x has domain of all real numbers and range (−π2,π2). To find the domain and range of inverse trigonometric functions, switch the domain and range of the original functions. Each graph of the inverse trigonometric function is a reflection of the graph of the original function about the line y=x.
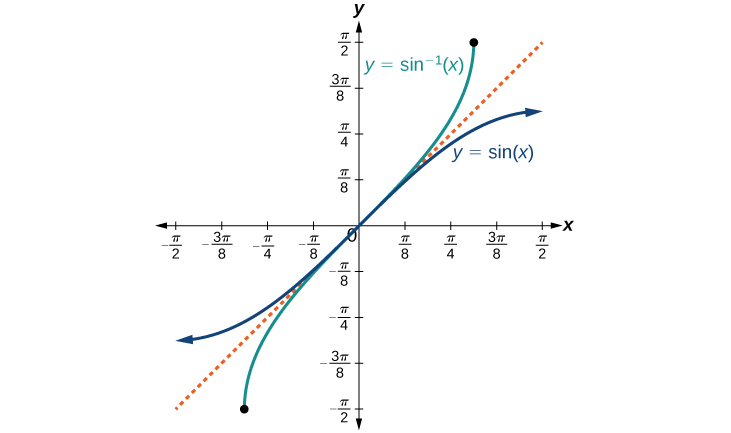
For angles in the interval [−π2,π2], if sin y=x, then sin−1x=y.
For angles in the interval [0,π], if cos y=x, then cos−1x=y.
For angles in the interval (−π2,π2), if tan y=x, then tan−1x=y.
Given sin(5π12)≈0.96593, write a relation involving the inverse sine.
Use the relation for the inverse sine. If sin y=x, then sin−1x=y .
In this problem, x=0.96593, and y=5π12.
Given cos(0.5)≈0.8776, write a relation involving the inverse cosine.
arccos(0.8776)≈0.5
Now that we can identify inverse functions, we will learn to evaluate them. For most values in their domains, we must evaluate the inverse trigonometric functions by using a calculator, interpolating from a table, or using some other numerical technique. Just as we did with the original trigonometric functions, we can give exact values for the inverse functions when we are using the special angles, specifically π6 (30°), π4 (45°), and π3 (60°), and their reflections into other quadrants.
Given a “special” input value, evaluate an inverse trigonometric function.
Evaluate each of the following.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?