| << Chapter < Page | Chapter >> Page > |
where s is defined to be the spin quantum number . This is very similar to the quantization of L given in L=√l(l+1)h2π , except that the only value allowed for s for electrons is 1/2.
The direction of intrinsic spin is quantized , just as is the direction of orbital angular momentum. The direction of spin angular momentum along one direction in space, again called the z -axis, can have only the values
for electrons. Sz is the z -component of spin angular momentum and ms is the spin projection quantum number . For electrons, s can only be 1/2, and ms can be either +1/2 or –1/2. Spin projection ms=+1/2 is referred to as spin up , whereas ms=−1/2 is called spin down . These are illustrated in [link] .
In later chapters, we will see that intrinsic spin is a characteristic of all subatomic particles. For some particles s is half-integral, whereas for others s is integral—there are crucial differences between half-integral spin particles and integral spin particles. Protons and neutrons, like electrons, have s=1/2 , whereas photons have s=1 , and other particles called pions have s=0 , and so on.
To summarize, the state of a system, such as the precise nature of an electron in an atom, is determined by its particular quantum numbers. These are expressed in the form (n, l,ml,ms) —see [link] For electrons in atoms , the principal quantum number can have the values n=1, 2, 3, ... . Once n is known, the values of the angular momentum quantum number are limited to l=1, 2, 3, ...,n−1 . For a given value of l , the angular momentum projection quantum number can have only the values ml=−l,−l+1, ...,−1, 0, 1, ...,l−1,l . Electron spin is independent of n, l, and ml , always having s=1/2 . The spin projection quantum number can have two values, ms=1/2or−1/2 .
| Name | Symbol | Allowed values |
|---|---|---|
| Principal quantum number | n | 1, 2, 3, ... |
| Angular momentum | l | 0, 1, 2, ...n−1 |
| Angular momentum projection | ml | −l,−l+1, ...,−1, 0, 1, ...,l−1,l(or0, ±1, ±2, ...,±l) |
| Spin The spin quantum number s is usually not stated, since it is always 1/2 for electrons | s | 1/2(electrons) |
| Spin projection | ms | −1/2,+1/2 |
[link] shows several hydrogen states corresponding to different sets of quantum numbers. Note that these clouds of probability are the locations of electrons as determined by making repeated measurements—each measurement finds the electron in a definite location, with a greater chance of finding the electron in some places rather than others. With repeated measurements, the pattern of probability shown in the figure emerges. The clouds of probability do not look like nor do they correspond to classical orbits. The uncertainty principle actually prevents us and nature from knowing how the electron gets from one place to another, and so an orbit really does not exist as such. Nature on a small scale is again much different from that on the large scale.
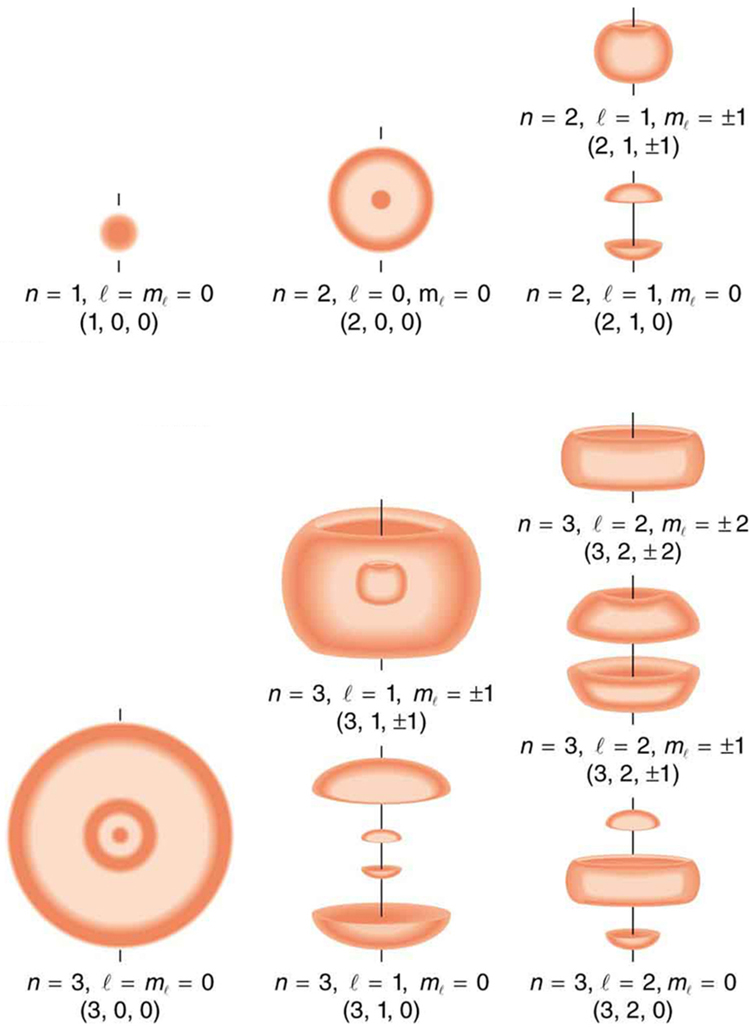
We will see that the quantum numbers discussed in this section are valid for a broad range of particles and other systems, such as nuclei. Some quantum numbers, such as intrinsic spin, are related to fundamental classifications of subatomic particles, and they obey laws that will give us further insight into the substructure of matter and its interactions.
The classic Stern-Gerlach Experiment shows that atoms have a property called spin. Spin is a kind of intrinsic angular momentum, which has no classical counterpart. When the z-component of the spin is measured, one always gets one of two values: spin up or spin down.

Define the quantum numbers n, l,ml, s , and ms .
For a given value of n , what are the allowed values of l ?
For a given value of l , what are the allowed values of ml ? What are the allowed values of ml for a given value of n ? Give an example in each case.
List all the possible values of s and ms for an electron. Are there particles for which these values are different? The same?
If an atom has an electron in the n=5 state with ml=3 , what are the possible values of l ?
l=4, 3 are possible since l<n and ∣ml∣≤l .
An atom has an electron with ml=2 . What is the smallest value of n for this electron?
What are the possible values of ml for an electron in the n=4 state?
n=4⇒l=3, 2, 1, 0⇒ml=±3,±2,±1, 0 are possible.
What, if any, constraints does a value of ml=1 place on the other quantum numbers for an electron in an atom?
(a) Calculate the magnitude of the angular momentum for an l=1 electron. (b) Compare your answer to the value Bohr proposed for the n=1 state.
(a) 1.49×10−34J⋅s
(b) 1.06×10−34J⋅s
(a) What is the magnitude of the angular momentum for an l=1 electron? (b) Calculate the magnitude of the electron’s spin angular momentum. (c) What is the ratio of these angular momenta?
Repeat [link] for l=3 .
(a) 3.66×10−34J⋅s
(b) s=9.13×10−35J⋅s
(c) LS=√12√3/4=4
(a) How many angles can L make with the z -axis for an l=2 electron? (b) Calculate the value of the smallest angle.
What angles can the spin S of an electron make with the z -axis?
θ=54.7º, 125.3º

Notification Switch
Would you like to follow the 'College physics' conversation and receive update notifications?