| << Chapter < Page | Chapter >> Page > |
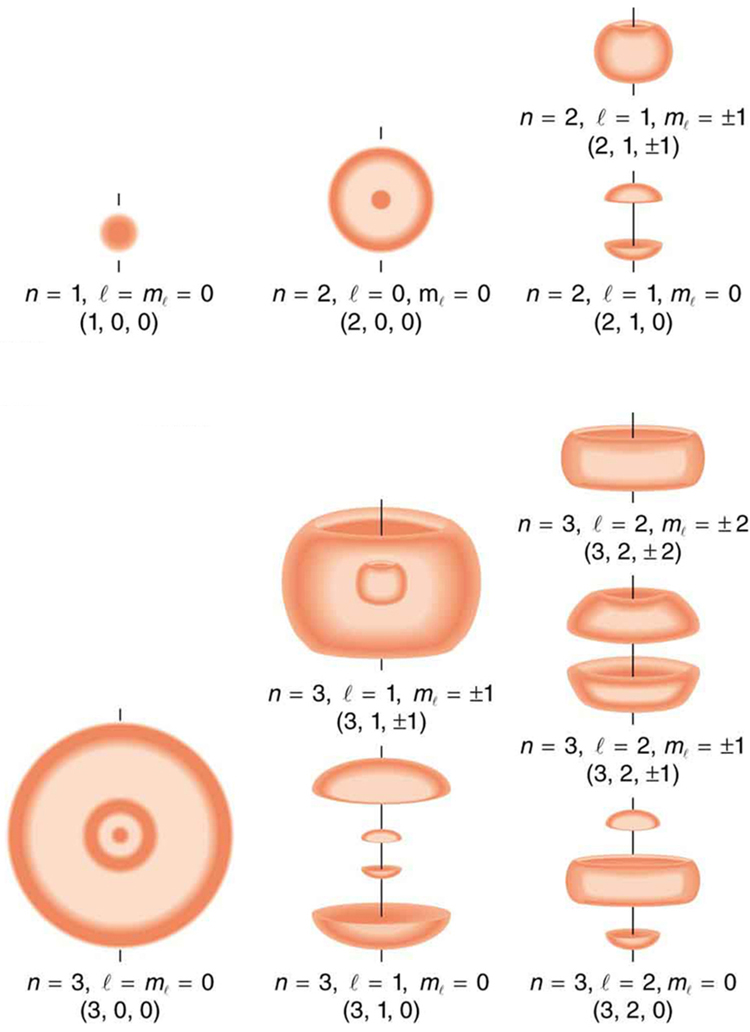
We will see that the quantum numbers discussed in this section are valid for a broad range of particles and other systems, such as nuclei. Some quantum numbers, such as intrinsic spin, are related to fundamental classifications of subatomic particles, and they obey laws that will give us further insight into the substructure of matter and its interactions.
The classic Stern-Gerlach Experiment shows that atoms have a property called spin. Spin is a kind of intrinsic angular momentum, which has no classical counterpart. When the z-component of the spin is measured, one always gets one of two values: spin up or spin down.

Define the quantum numbers n, l,ml, s , and ms .
For a given value of n , what are the allowed values of l ?
For a given value of l , what are the allowed values of ml ? What are the allowed values of ml for a given value of n ? Give an example in each case.
List all the possible values of s and ms for an electron. Are there particles for which these values are different? The same?
If an atom has an electron in the n=5 state with ml=3 , what are the possible values of l ?
l=4, 3 are possible since l<n and ∣ml∣≤l .
An atom has an electron with ml=2 . What is the smallest value of n for this electron?
What are the possible values of ml for an electron in the n=4 state?
n=4⇒l=3, 2, 1, 0⇒ml=±3,±2,±1, 0 are possible.
What, if any, constraints does a value of ml=1 place on the other quantum numbers for an electron in an atom?
(a) Calculate the magnitude of the angular momentum for an l=1 electron. (b) Compare your answer to the value Bohr proposed for the n=1 state.
(a) 1.49×10−34J⋅s
(b) 1.06×10−34J⋅s
(a) What is the magnitude of the angular momentum for an l=1 electron? (b) Calculate the magnitude of the electron’s spin angular momentum. (c) What is the ratio of these angular momenta?
Repeat [link] for l=3 .
(a) 3.66×10−34J⋅s
(b) s=9.13×10−35J⋅s
(c) LS=√12√3/4=4
(a) How many angles can L make with the z -axis for an l=2 electron? (b) Calculate the value of the smallest angle.
What angles can the spin S of an electron make with the z -axis?
θ=54.7º, 125.3º

Notification Switch
Would you like to follow the 'College physics for ap® courses' conversation and receive update notifications?