| << Chapter < Page | Chapter >> Page > |
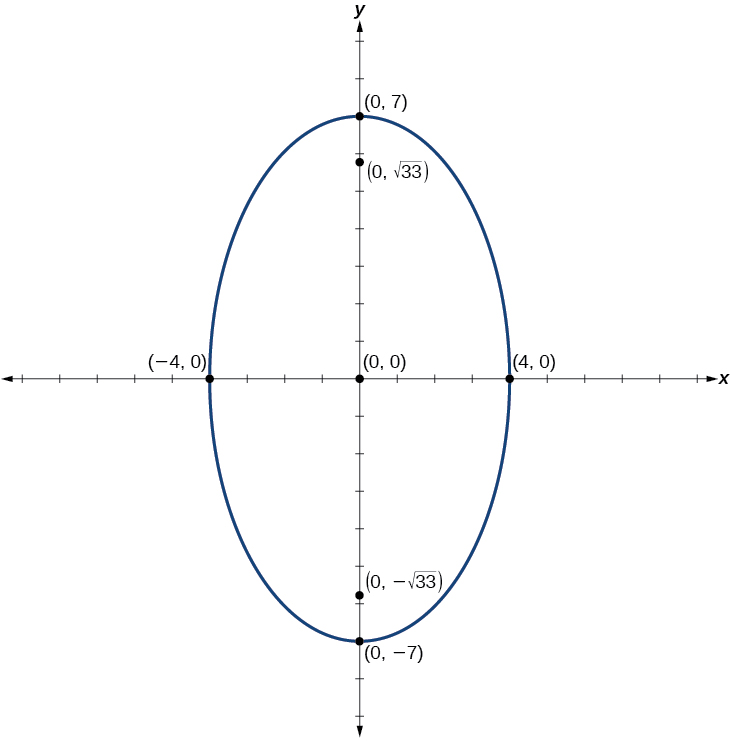
Graph the ellipse given by the equation 49x2+16y2=784. Rewrite the equation in standard form. Then identify and label the center, vertices, co-vertices, and foci.
Standard form: x216+y249=1; center: (0,0); vertices: (0,±7); co-vertices: (±4,0); foci: (0,±√33)
When an ellipse is not centered at the origin, we can still use the standard forms to find the key features of the graph. When the ellipse is centered at some point, (h,k), we use the standard forms (x−h)2a2+(y−k)2b2=1, a>b for horizontal ellipses and (x−h)2b2+(y−k)2a2=1, a>b for vertical ellipses. From these standard equations, we can easily determine the center, vertices, co-vertices, foci, and positions of the major and minor axes.
Given the standard form of an equation for an ellipse centered at (h,k), sketch the graph.
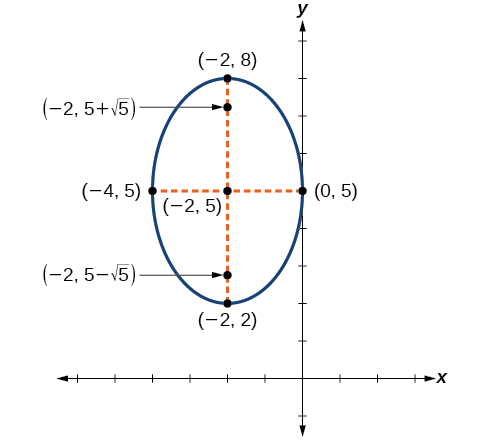
Graph the ellipse given by the equation, (x+2)24+(y−5)29=1. Identify and label the center, vertices, co-vertices, and foci.
First, we determine the position of the major axis. Because 9>4, the major axis is parallel to the y -axis. Therefore, the equation is in the form (x−h)2b2+(y−k)2a2=1, where b2=4 and a2=9. It follows that:
Therefore, the coordinates of the foci are (−2,5−√5) and (−2,5+√5).
Next, we plot and label the center, vertices, co-vertices, and foci, and draw a smooth curve to form the ellipse.
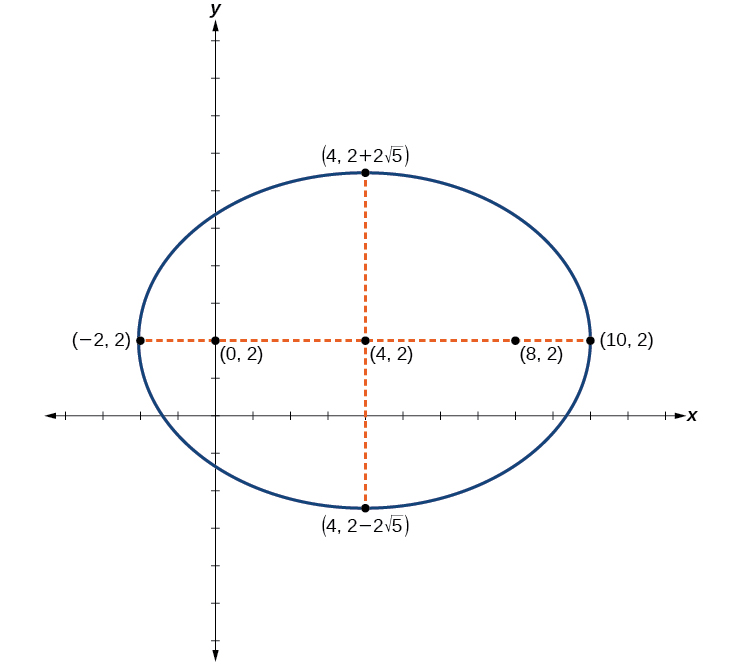
Graph the ellipse given by the equation (x−4)236+(y−2)220=1. Identify and label the center, vertices, co-vertices, and foci.
Center: (4,2); vertices: (−2,2) and (10,2); co-vertices: (4,2−2√5) and (4,2+2√5); foci: (0,2) and (8,2)
Given the general form of an equation for an ellipse centered at ( h , k ), express the equation in standard form.

Notification Switch
Would you like to follow the 'College algebra' conversation and receive update notifications?